Numerical Integration#
Teng-Jui Lin
Content adapted from UW AMATH 301, Beginning Scientific Computing, in Spring 2020.
Numerical integration
First order methods
Left endpoint rule
Right endpoint rule
Second order methods
Midpoint rule
Trapezoidal rule
Fourth order method
Simpson’s rule
Errors
scipyimplementationsSolving single integral by
scipy.integrate.quad()Solving double integral by
scipy.integrate.dblquad()Solving triple integral by
scipy.integrate.tplquad()Reference:
scipy.integrateintegration tutorial
Numerical integration algorithms#
Suppose we have data points (or function values) with domain
The left endpoint rule uses left endpoint’s height to approximate the area under the curve as rectangles, having
The right endpoint rule uses right endpoint’s height to approximate the area under the curve as rectangles, having
The midpoint rule uses the midpoint’s height to approximate the area under the curve as rectangles, having
The trapezoidal rule uses the left and right endpoints’ height to approximate the area under the curve as trapezoids, giving a linear approximation to the “extra area,” having
Simpson’s rule uses the left and right endpoints’ height to approximate the area under the curve using a quadratic approximation to the “extra area” (although having same error with cubic polynomial), having
Note that Simpson’s rule can only have even subintervals
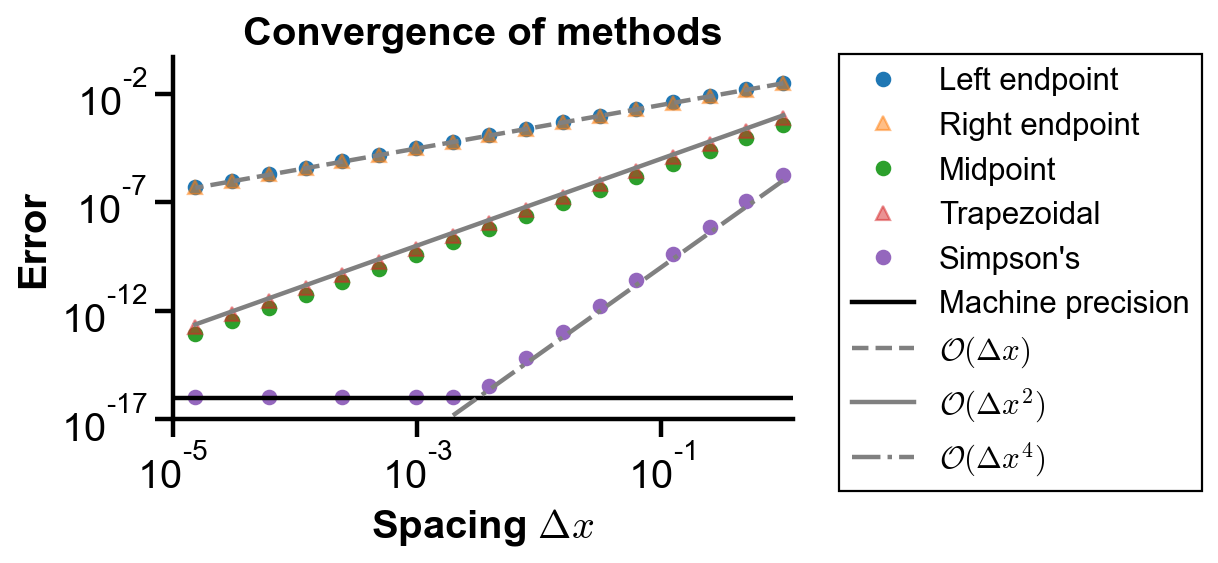
The local and global errors of each method is shown below:
Method |
Local Error |
Global Error |
|---|---|---|
Left endpoint rule |
||
Right endpoint rule |
||
Midpoint rule |
||
Trapezoidal rule |
||
Simpson’s rule |
Implementation#
Problem Statement. Huskies has have weights that are normally distributed with a mean of 85 pounds and a standard deviation of 5 pounds. The probability of randomly selected Malamute having a weight between 76 and 86 pounds is
Evaluate the integral using left endpoint, right endpoint, midpoint, trapezoidal, and Simpson’s rule using a spacing of scipy.integrate.quad().
import numpy as np
import matplotlib.pyplot as plt
import scipy
from scipy import integrate
# define target function
p_density = lambda x : 1/np.sqrt(50*np.pi) * np.exp(-(x-85)**2 / 50)
# define parameters
left_bound = 76
right_bound = 86
dx = 0.1
# "exact" solution
scipy_soln = scipy.integrate.quad(p_density, left_bound, right_bound)[0]
scipy_soln
0.5433293903261772
# left endpoint rule
x_left = np.arange(left_bound, right_bound+dx/2, dx)
y_left = p_density(x_left)
left_soln = dx * np.sum(y_left[:-1])
left_soln
0.5402011209647617
# right endpoint rule
x_right = np.arange(left_bound, right_bound+dx/2, dx)
y_right = p_density(x_right)
right_soln = dx * np.sum(y_right[1:])
right_soln
0.5464429716782531
# midpoint rule
x_mid_ends = np.arange(left_bound, right_bound+dx/2, dx)
x_mid = (x_mid_ends[:-1] + x_mid_ends[1:])/2
y_mid = p_density(x_mid)
mid_soln = dx * np.sum(y_mid)
mid_soln
0.5433330623449413
# trapezoidal rule
x_trap = np.arange(left_bound, right_bound+dx/2, dx)
y_trap = p_density(x_trap)
trap_soln = dx/2 * (y_trap[0] + 2*np.sum(y_trap[1:-1]) + y_trap[-1])
trap_soln
0.5433220463215073
# simpson's rule
x_simps = np.arange(left_bound, right_bound+dx/2, dx)
y_simps = p_density(x_simps)
simps_soln = dx/3 * (y_simps[0] + 4*np.sum(y_simps[1:-1:2]) + 2*np.sum(y_simps[2:-2:2]) + y_simps[-1])
simps_soln
0.5433293905016291
Order of different methods#
Problem Statement. Huskies has have weights that are normally distributed with a mean of 85 pounds and a standard deviation of 5 pounds. The probability of randomly selected Malamute having a weight between 76 and 86 pounds is
Evaluate the integral using left endpoint, right endpoint, midpoint, trapezoidal, and Simpson’s rule using different scipy.integrate.quad().
# define target function
p_density = lambda x : 1/np.sqrt(50*np.pi) * np.exp(-(x-85)**2 / 50)
# define parameters
left_bound = 76
right_bound = 86
dx = 2.0**np.arange(0, -16-0.5, -1)
# "exact" solution
scipy_soln = scipy.integrate.quad(p_density, left_bound, right_bound)[0]
scipy_soln
0.5433293903261772
# left endpoint rule
left_solns = np.zeros(len(dx))
left_error = np.zeros(len(dx))
for i in range(len(dx)):
x_left = np.arange(left_bound, right_bound+dx[i]/2, dx[i])
y_left = p_density(x_left)
left_solns[i] = dx[i] * np.sum(y_left[:-1])
left_error[i] = abs(scipy_soln - left_solns[i])
# right endpoint rule
right_solns = np.zeros(len(dx))
right_error = np.zeros(len(dx))
for i in range(len(dx)):
x_right = np.arange(left_bound, right_bound+dx[i]/2, dx[i])
y_right = p_density(x_right)
right_solns[i] = dx[i] * np.sum(y_right[1:])
right_error[i] = abs(scipy_soln - right_solns[i])
# midpoint rule
mid_solns = np.zeros(len(dx))
mid_error = np.zeros(len(dx))
for i in range(len(dx)):
x_mid_ends = np.arange(left_bound, right_bound+dx[i]/2, dx[i])
x_mid = (x_mid_ends[:-1] + x_mid_ends[1:])/2
y_mid = p_density(x_mid)
mid_solns[i] = dx[i] * np.sum(y_mid)
mid_error[i] = abs(scipy_soln - mid_solns[i])
# trapezoidal rule
trap_solns = np.zeros(len(dx))
trap_error = np.zeros(len(dx))
for i in range(len(dx)):
x_trap = np.arange(left_bound, right_bound+dx[i]/2, dx[i])
y_trap = p_density(x_trap)
trap_solns[i] = dx[i]/2 * (y_trap[0] + 2*np.sum(y_trap[1:-1]) + y_trap[-1])
trap_error[i] = abs(scipy_soln - trap_solns[i])
# simpson's rule
simps_solns = np.zeros(len(dx))
simps_error = np.zeros(len(dx))
for i in range(len(dx)):
x_simps = np.arange(left_bound, right_bound+dx[i]/2, dx[i])
y_simps = p_density(x_simps)
simps_solns[i] = dx[i]/3 * (y_simps[0] + 4*np.sum(y_simps[1:-1:2]) + 2*np.sum(y_simps[2:-2:2]) + y_simps[-1])
simps_error[i] = abs(scipy_soln - simps_solns[i])
# plot settings
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.rcParams.update({
'font.family': 'Arial', # Times New Roman, Calibri
'font.weight': 'normal',
'mathtext.fontset': 'cm',
'font.size': 18,
'lines.linewidth': 2,
'axes.linewidth': 2,
'axes.spines.top': False,
'axes.spines.right': False,
'axes.titleweight': 'bold',
'axes.titlesize': 18,
'axes.labelweight': 'bold',
'xtick.major.size': 8,
'xtick.major.width': 2,
'ytick.major.size': 8,
'ytick.major.width': 2,
'figure.dpi': 80,
'legend.framealpha': 1,
'legend.edgecolor': 'black',
'legend.fancybox': False,
'legend.fontsize': 14
})
fig, ax = plt.subplots(figsize=(5, 3))
ax.loglog(dx, left_error, 'o', alpha=1, label='Left endpoint')
ax.loglog(dx, right_error, '^', alpha=0.5, label='Right endpoint')
ax.loglog(dx, mid_error, 'o', alpha=1, label='Midpoint')
ax.loglog(dx, trap_error, '^', alpha=0.5, label='Trapezoidal')
ax.loglog(dx, simps_error, 'o', alpha=1, label='Simpson\'s')
ax.loglog([1e-5, 1.2], [1e-16, 1e-16], color='black', label='Machine precision')
ax.loglog(dx, 3e-2*dx, '--', alpha=1, color='gray', label='$\mathcal{O}(\Delta x)$')
ax.loglog(dx, 1e-3*dx**2, '-', alpha=1, color='gray', label='$\mathcal{O}(\Delta x^2)$')
ax.loglog(dx, 1e-6*dx**4, '-.', alpha=1, color='gray', label='$\mathcal{O}(\Delta x^4)$')
ax.set_xlabel('Spacing $\Delta x$')
ax.set_ylabel('Error')
ax.set_title('Convergence of methods')
ax.set_xlim(1e-5, 1.2)
ax.set_ylim(1e-17)
ax.legend(loc='upper left', bbox_to_anchor=(1.05, 1.05))
<matplotlib.legend.Legend at 0x1a14949b6c8>
Numerical integration with scipy.integrate#
Problem Statement. Find the following integrals using commands in scipy.integrate and compare with analytical solution.
Single integral uses quad(); double integral uses dblquad(); triple integral uses tplquad().
# single integral
func_single = lambda x : np.exp(-x**2)
lower_bound = -np.inf
upper_bound = np.inf
result_single = scipy.integrate.quad(func_single, lower_bound, upper_bound)[0]
result_single
1.7724538509055159
# error of single integral
analytic_single = np.sqrt(np.pi)
error_single = abs(analytic_single - result_single)
error_single
0.0
# double integral
func_double = lambda x, y : x*y # order of x, y as in dx dy
x_lower = lambda y : 0.5*y**2 - 3
x_upper = lambda y : y+1
y_lower = -2
y_upper = 4
result_double = scipy.integrate.dblquad(func_double,
y_lower, y_upper,
x_lower, x_upper)[0] # order of bounds from left to right
result_double
35.99999999999999
# error of double integral
analytic_double = 36
error_double = abs(analytic_double - result_double)
error_double
7.105427357601002e-15
# triple integral
func_triple = lambda z, y, x : x**2 + y**2 # order of z, y, x as in dz, dy, dx
x_lower = -2
x_upper = 2
y_lower = lambda x : -np.sqrt(4 - x**2)
y_upper = lambda x : np.sqrt(4 - x**2)
z_lower = lambda x, y : np.sqrt(x**2 + y**2)
z_upper = lambda x, y : 2
result_triple = scipy.integrate.tplquad(func_triple,
x_lower, x_upper,
y_lower, y_upper,
z_lower, z_upper)[0] # order of bounds from left to right
result_triple
10.053096491479954
# error of triple integral
analytic_triple = 16 / 5 * np.pi
error_triple = abs(analytic_triple - result_triple)
error_triple
7.384315381386841e-12

