Chaotic Systems

Teng-Jui Lin

Content from UW AMATH 301, Beginning Scientific Computing. Although not covered in Spring 2020, the topic is presented in previous years: (1) Application of Runge-Kutta to Lorenz Equation, (2) Vectorized Time-step Integrators.

• Chaotic system

  • Lorenz system

    • One initial condition

    • Two close but distinct initial conditions

    • A cube of initial conditions

  • Visialization techniques

    • Interactive plotting

    • Animations

Lorenz system

The Lorenz system is a system of nonlinear ODEs developed by Edward Lorenz in 1963 to model atmospheric convection. The system

\[\begin{split} \begin{aligned} \dot{x} &= \sigma (y-x) \\ \dot{y} &= x(\rho-z) - y \\ \dot{z} &= xy - \beta z \end{aligned} \end{split}\]

with parameters \(\sigma = 10, \rho = 28, \beta = 8/3\) can lead to chaotic behavior, where the behavior is unpredictable and sensitive to initial condition and error accumulation.

One initial condition

Problem Statement. Solve the Lorenz system with the initial condition of \(x(0) = -8, y(0) = 8, z(0) = 27\) for \(t \in [0, 100]\) with \(\Delta t = 0.01\) using the above parameters.

• Generate a static plot of all the trajectory in the time interval.

• Generate a rotating animation of all the trajectory in the time interval.

• Generate an animation of the trajectory over time.

Note on animation: for local reproducible results, download ffmpeg and add to path variable. For reproducible results online, use Google Colab and run the command below.

# Run the command in Google Colab for reproducible results online
# !apt install ffmpeg

Solving the system and static plot

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import scipy
from scipy import integrate

# Lorenz's chaotic parameters
sigma = 10
rho = 28
beta = 8/3

# initial conditions
initial_val = np.array([-8, 8, 27])

# time array
t_initial = 0
t_final = 100
dt = 0.01
t = np.arange(t_initial, t_final+dt/2, dt)
t_len = len(t)

# define ode system
dxdt = lambda x, y, z : sigma*(y - x)
dydt = lambda x, y, z : x*(rho - z) - y
dzdt = lambda x, y, z : x*y - beta*z
ode_syst = lambda t, v : np.array([dxdt(*v), dydt(*v), dzdt(*v)])

# solve ode system
ode_soln = scipy.integrate.solve_ivp(ode_syst, [t_initial, t_final], initial_val, t_eval=t).y

# plot settings
%config InlineBackend.figure_format = 'retina'
%matplotlib inline

plt.rcParams.update({
    'font.family': 'Arial',  # Times New Roman, Calibri
    'font.weight': 'normal',
    'mathtext.fontset': 'cm',
    'font.size': 18,
    
    'lines.linewidth': 2,
    
    'axes.linewidth': 2,
    'axes.spines.top': False,
    'axes.spines.right': False,
    'axes.titleweight': 'bold',
    'axes.titlesize': 18,
    'axes.labelweight': 'bold',
    
    'xtick.major.size': 8,
    'xtick.major.width': 2,
    'ytick.major.size': 8,
    'ytick.major.width': 2,
    
    'figure.dpi': 80,
    'savefig.dpi': 300,
    
    'legend.framealpha': 1, 
    'legend.edgecolor': 'black',
    'legend.fancybox': False,
    'legend.fontsize': 14,
    
    'animation.html': 'html5',
})

# plot 3d visualization
plt.rcParams.update({'xtick.labelsize': 18,})
fig, ax = plt.subplots(figsize=(5, 5), subplot_kw={"projection": "3d"})
ax.plot(*ode_soln, '.', color='black', alpha=0.5)

# plot settings
ax.set_xlabel('$x$', fontsize=18, labelpad=20)
ax.set_ylabel('$y$', fontsize=18, labelpad=20)
ax.set_zlabel('$z$', fontsize=18, labelpad=20)
ax.set_title(f'Lorenz\'s Equation \n $\sigma={sigma}, \\beta={beta :.1f}, \\rho={rho}$', fontsize=18, y=1)
ax.set_xlim(-25, 25)
ax.set_ylim(-25, 25)
ax.set_zlim(0, 50)
ax.view_init(30, -45)  # viewing angle
ax.dist = 13  # zoom out to fit all labels in

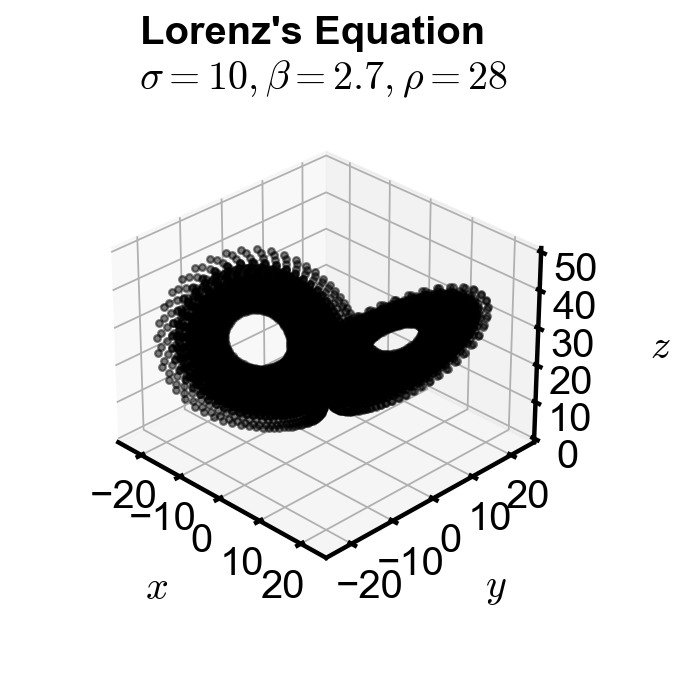
Rotating animation of all trajectory

# plot static portion
fig, ax = plt.subplots(figsize=(7, 7), subplot_kw={"projection": "3d"})
ax.plot(*ode_soln, '.', color='black', alpha=0.5)
ax.set_xlim(-25, 25)
ax.set_ylim(-25, 25)
ax.set_zlim(0, 50)
ax.set_axis_off()

def draw_frame(n):
    '''
    Commands to update parameters.
    Here, the viewing angle changes each frame.
    '''
    ax.view_init(elev=0, azim=360*n/(frame_num))
    return fig,

# create animation of given time length
# note here we fit all the data points into the given animation time
from matplotlib import animation
anim_time = 4  # s
fps = 60
frame_num = int(fps * anim_time)
anim = animation.FuncAnimation(fig, draw_frame, frames=frame_num, interval=1000/fps, blit=True)

plt.close()  # disable showing initial frame

# convert animation to video (time-limiting step)
from IPython.display import HTML
HTML(anim.to_html5_video() + '<style>video{width: 400px !important; height: auto;}</style>')

Animation of trajectory over time

# interactive plot
%matplotlib qt

# plot static portion
fig, ax = plt.subplots(figsize=(7, 7), subplot_kw={"projection": "3d"})
ax.set_xlim(-25, 25)
ax.set_ylim(-25, 25)
ax.set_zlim(0, 50)
ax.set_axis_off()

# plot empty framework
points, = ax.plot([], [], [], '.', color='black', alpha=0.5)
title = ax.set_title('')

# update changes each frame
for n in range(frame_num):
    time_points = round(t_len/frame_num)
    points.set_data(ode_soln[:2, :time_points*n+time_points])
    points.set_3d_properties(ode_soln[2, :time_points*n+time_points])
    title.set_text(f't = {t[n] :.3f}')
    plt.pause(0.0001)

# back to static plot and animations
%matplotlib inline

# plot static portion
fig, ax = plt.subplots(figsize=(7, 7), subplot_kw={"projection": "3d"})
ax.set_xlim(-25, 25)
ax.set_ylim(-25, 25)
ax.set_zlim(0, 50)
ax.set_axis_off()

# plot empty framework
points, = ax.plot([], [], [], '.', color='black', alpha=0.5)
title = ax.set_title('')

def draw_frame(n):
    '''
    Commands to update parameters.
    Here, the 3d data points changes each frame.
    '''
    num_points = round(t_len/frame_num)
    points.set_data(ode_soln[:2, :num_points*n+num_points])
    points.set_3d_properties(ode_soln[2, :num_points*n+num_points])
    title.set_text(f't = {t[n] :.3f}')
    return fig,

# create animation of given time length
# note here we fit all the data points into the given animation time
from matplotlib import animation
anim_time = 4  # s
fps = 60
frame_num = int(fps * anim_time)
anim = animation.FuncAnimation(fig, draw_frame, frames=frame_num, interval=1000/fps, blit=True)

plt.close()  # disable showing initial frame

# convert animation to video (time-limiting step)
from IPython.display import HTML
HTML(anim.to_html5_video() + '<style>video{width: 400px !important; height: auto;}</style>')

Two initial conditions

Because Lorenz system with the above parameter is a chaotic system, it is sensitive to changes in initial conditions and error accumulation. We show this using the trajectory of two close but distinct initial conditions.

Problem Statement. Solve the Lorenz system with the two initial conditions of

• \(x(0) = -8, y(0) = 8, z(0) = 27\)

• \(x(0) = -8.01, y(0) = 8, z(0) = 27\)

for \(t \in [0, 100]\) with \(\Delta t = 0.01\) using the above parameters.

• Generate a static plot of all the trajectory in the time interval.

• Generate an rotating animation of all the trajectory in the time interval.

• Generate an interactive plot of the trajectory over time. Save the the interactive plot as an animation.

Solving the systems and static plot

# Lorenz's chaotic parameters
sigma = 10
rho = 28
beta = 8/3

# initial conditions
initial_val1 = np.array([-8, 8, 27])
initial_val2 = np.array([-8.01, 8, 27])

# time array
t_initial = 0
t_final = 100
dt = 0.01
t = np.arange(t_initial, t_final+dt/2, dt)
t_len = len(t)

# define ode system
dxdt = lambda x, y, z : sigma*(y - x)
dydt = lambda x, y, z : x*(rho - z) - y
dzdt = lambda x, y, z : x*y - beta*z
ode_syst = lambda t, v : np.array([dxdt(*v), dydt(*v), dzdt(*v)])

# solve ode system
ode_soln1 = scipy.integrate.solve_ivp(ode_syst, [t_initial, t_final], initial_val1, t_eval=t).y
ode_soln2 = scipy.integrate.solve_ivp(ode_syst, [t_initial, t_final], initial_val2, t_eval=t).y

# plot 3d visualization
plt.rcParams.update({'xtick.labelsize': 18,})
fig, ax = plt.subplots(figsize=(5, 5), subplot_kw={"projection": "3d"})
ax.plot(*ode_soln1, '.', alpha=0.7)
ax.plot(*ode_soln2, '.', alpha=0.1)

# plot settings
ax.set_xlabel('$x$', fontsize=18, labelpad=20)
ax.set_ylabel('$y$', fontsize=18, labelpad=20)
ax.set_zlabel('$z$', fontsize=18, labelpad=20)
ax.set_title(f'Lorenz\'s Equation \n $\sigma={sigma}, \\beta={beta :.1f}, \\rho={rho}$', fontsize=18, y=1)
ax.set_xlim(-25, 25)
ax.set_ylim(-25, 25)
ax.set_zlim(0, 50)
ax.view_init(30, -45)  # viewing angle
ax.dist = 13  # zoom out to fit all labels in

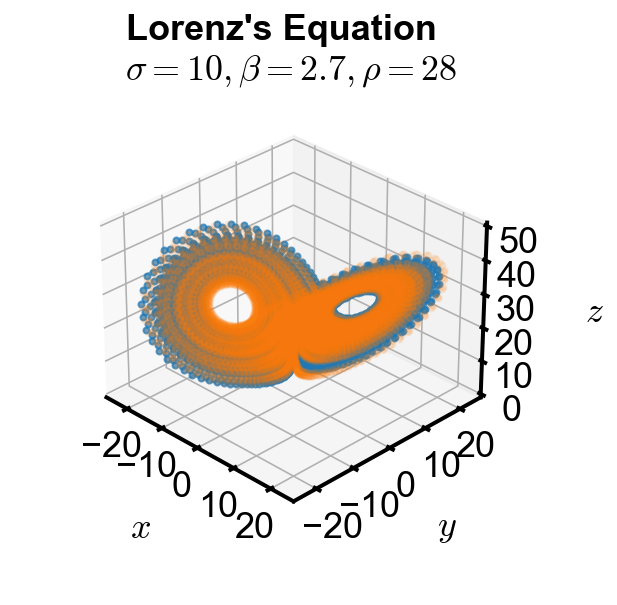
Rotating animation of all trajectory

# plot static portion
fig, ax = plt.subplots(figsize=(7, 7), subplot_kw={"projection": "3d"})
ax.plot(*ode_soln1, '.', alpha=0.7)
ax.plot(*ode_soln2, '.', alpha=0.1)
ax.set_xlim(-25, 25)
ax.set_ylim(-25, 25)
ax.set_zlim(0, 50)
ax.set_axis_off()

def draw_frame(n):
    '''
    Commands to update parameters.
    Here, the viewing angle changes each frame.
    '''
    ax.view_init(elev=0, azim=360*n/(frame_num))
    return fig,

# create animation of given time length
# note here we fit all the data points into the given animation time
from matplotlib import animation
anim_time = 4  # s
fps = 60
frame_num = int(fps * anim_time)
anim = animation.FuncAnimation(fig, draw_frame, frames=frame_num, interval=1000/fps, blit=True)

plt.close()  # disable showing initial frame

# convert animation to video (time-limiting step)
from IPython.display import HTML
HTML(anim.to_html5_video() + '<style>video{width: 400px !important; height: auto;}</style>')

Interactive plot and animation of trajectory over time

# interactive plot
%matplotlib qt

# plot static portion
fig, ax = plt.subplots(figsize=(7, 7), subplot_kw={"projection": "3d"})
ax.set_xlim(-25, 25)
ax.set_ylim(-25, 25)
ax.set_zlim(0, 50)
ax.set_axis_off()

# plot empty framework
points1, = ax.plot([], [], [], '.', alpha=0.7)
points2, = ax.plot([], [], [], '.', alpha=0.1)
title = ax.set_title('')

# update changes each frame
for n in range(frame_num):
    time_points = round(t_len/frame_num)
    points1.set_data(ode_soln1[:2, :time_points*n+time_points])
    points1.set_3d_properties(ode_soln1[2, :time_points*n+time_points])
    points2.set_data(ode_soln2[:2, :time_points*n+time_points])
    points2.set_3d_properties(ode_soln2[2, :time_points*n+time_points])
    title.set_text(f't = {t[n] :.3f}')
    plt.pause(0.00001)

# back to static plot and animations
%matplotlib inline

# plot static portion
fig, ax = plt.subplots(figsize=(7, 7), subplot_kw={"projection": "3d"})
ax.set_xlim(-25, 25)
ax.set_ylim(-25, 25)
ax.set_zlim(0, 50)
ax.set_axis_off()

# plot empty framework
points1, = ax.plot([], [], [], '.', alpha=0.7)
points2, = ax.plot([], [], [], '.', alpha=0.1)
title = ax.set_title('')

def draw_frame(n):
    '''
    Commands to update parameters.
    Here, the 3d data points and title changes each frame.
    '''
    time_points = round(t_len/frame_num)
    points1.set_data(ode_soln1[:2, :time_points*n+time_points])
    points1.set_3d_properties(ode_soln1[2, :time_points*n+time_points])
    points2.set_data(ode_soln2[:2, :time_points*n+time_points])
    points2.set_3d_properties(ode_soln2[2, :time_points*n+time_points])
    title.set_text(f't = {t[n] :.3f}')
    return fig,

# create animation of given time length
# note here we fit all the data points into the given animation time
from matplotlib import animation
anim_time = 4  # s
fps = 60
frame_num = int(fps * anim_time)
anim = animation.FuncAnimation(fig, draw_frame, frames=frame_num, interval=1000/fps, blit=True)

plt.close()  # disable showing initial frame

# convert animation to video (time-limiting step)
from IPython.display import HTML
HTML(anim.to_html5_video() + '<style>video{width: 400px !important; height: auto;}</style>')

The above three plots/animations demonstrates that even with very small change in initial conditions, the chaotic nature of the Lorenz system gives vastly different trajectories.