Neuron Excitation Model 3

Teng-Jui Lin

Content adapted from UW AMATH 301, Beginning Scientific Computing. Although not covered in Spring 2020, the topic is presented in previous years.

• Phase portraits

  • FitzHugh-Nagumo neuron excitation model (continued)

    • Exploration: oscillating external current

FitzHugh-Nagumo neuron excitation model (review)

Let \(v\) be the membrane voltage, and let \(w\) be the activity of several types of membrane channel proteins. The FitzHugh-Nagumo model describes the excitation of neuron membrane over time with the system of ODEs

\[\begin{split} \begin{aligned} \dot{v} &= v - \dfrac{1}{3}v^3-w+I(t) \\ \dot{w} &= \dfrac{a+v-bw}{\tau} \end{aligned} \end{split}\]

with an external electrical current \(I(t)\). The constant parameters \(a, b, \tau\) controls the activity of channel proteins.

Note on animation: for local reproducible results, download ffmpeg and add to path variable. For reproducible results online, use Google Colab and run the command below.

# Run the command in Google Colab for reproducible results online
# !apt install ffmpeg

import numpy as np
import matplotlib.pyplot as plt
import scipy
from scipy import integrate

def custom_plot_settings():
    %config InlineBackend.figure_format = 'retina'
    %matplotlib inline

    plt.rcParams.update({
        'font.family': 'Arial',  # Times New Roman, Calibri
        'font.weight': 'normal',
        'mathtext.fontset': 'cm',
        'font.size': 18,

        'lines.linewidth': 2,

        'axes.linewidth': 2,
        'axes.spines.top': False,
        'axes.spines.right': False,
        'axes.titleweight': 'bold',
        'axes.titlesize': 18,
        'axes.labelweight': 'bold',

        'xtick.major.size': 8,
        'xtick.major.width': 2,
        'ytick.major.size': 8,
        'ytick.major.width': 2,

        'figure.dpi': 80,
        'savefig.dpi': 300,

        'legend.framealpha': 1, 
        'legend.edgecolor': 'black',
        'legend.fancybox': False,
        'legend.fontsize': 14,

        'animation.html': 'html5',
    })

custom_plot_settings()

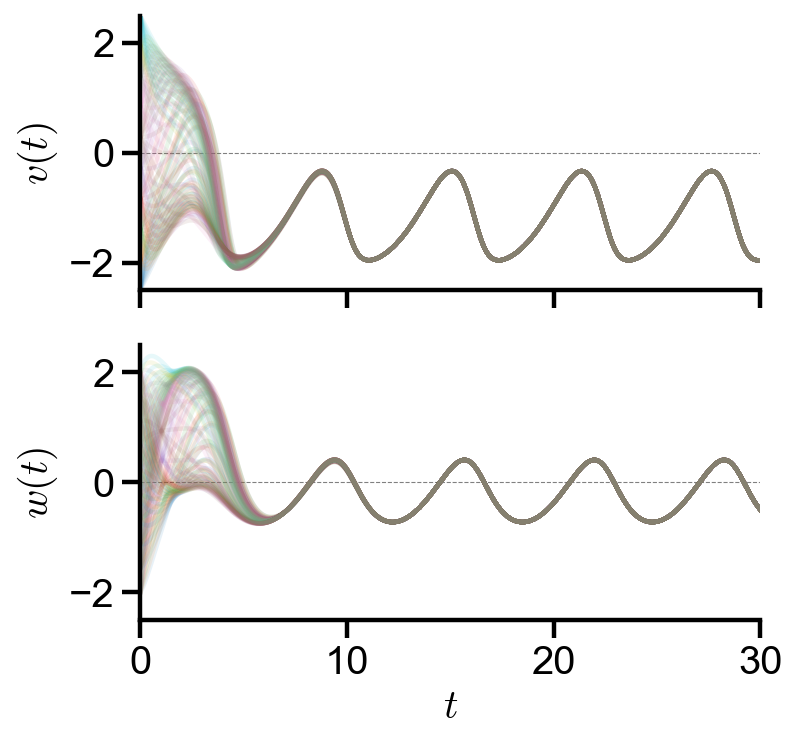
Exploration: oscillating external current

Problem Statement. With the initial conditions of \(v(0) = 1\) and \(w(0) = 0\), solve the FitzHugh-Nagumo model with parameters \(a=1, b=1, \tau=1\) and constant external current of

\[ I(t) = \sin(t) \]

• Generate plots of \(v(t)\) and \(w(t)\) over time in the intervals \(t \in [0, 15]\) and \(t \in [0, 5]\).

• Generate an animated phase portrait over time in the intervals \(t \in [0, 15]\) and \(t \in [0, 5]\).

# model params
a = 1
b = 1
tau = 1

# time array
t_initial = 0
t_final = 30
t = np.linspace(t_initial, t_final, 1000)
t_len = len(t)

# ode system
I = lambda t : np.sin(t)
dvdt = lambda t, v, w : v - 1/3*v**3 - w + I(t)
dwdt = lambda t, v, w : (a + v - b*w) / tau
ode_syst = lambda t, z : np.array([dvdt(t, *z), dwdt(t, *z)])

# grid of initial conditions
initial_vvec = np.linspace(-2.5, 2.5, 10)
initial_wvec = np.linspace(-2, 2, 10)
initial_vals = np.meshgrid(initial_vvec, initial_wvec)
initial_vals = np.array([initial_vals[0].reshape(-1), initial_vals[1].reshape(-1)]).T

# ode soln for grid of initial conditions
ode_solns = [0]*len(initial_vals)
for i in range(len(initial_vals)):
    ode_solns[i] = scipy.integrate.solve_ivp(ode_syst, [t_initial, t_final], initial_vals[i], t_eval=t).y
ode_solns = np.array(ode_solns)

# quiver grid
vvec = np.linspace(-2.5, 2.5, 20)
wvec = np.linspace(-2, 2, 20)
V, W = np.meshgrid(vvec, wvec)
custom_plot_settings()

fig, axs = plt.subplots(2, 1, figsize=(5, 5), sharex=True)
axs[0].set_ylabel('$v(t)$')
axs[1].set_ylabel('$w(t)$')
axs[1].set_xlabel('$t$')

for i in range(len(initial_vals)):
    axs[0].plot(t, ode_solns[i, 0], label='$v(t)$', alpha=0.1)
    axs[1].plot(t, ode_solns[i, 1], label='$w(t)$', alpha=0.1)

for i in range(2):
    axs[i].plot([t_initial, t_final], [0, 0], '--', color='grey', lw=0.5, zorder=0)  # zero ref
    axs[i].set_xlim(t_initial, t_final)
    axs[i].set_ylim(-2.5, 2.5)

def make_animation(t_range=t_len, anim_time=4, fps=60, xmin=-2.5, xmax=2.5, ymin=-2, ymax=2):
    '''
    This function is notebook-specific and not meant to generalize to other settings.
    Makes animation of time-dependent phase portrait.
    Warning: Many parameters are taken from the global namespace. They need to be defined before use.
    '''
    # back to static plot and animations
    custom_plot_settings()

    # plot static portion
    fig, ax = plt.subplots(figsize=(5, 5))
    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)
    ax.set_xlabel('$v(t)$')
    ax.set_ylabel('$w(t)$')
    plt.tight_layout()

    # plot empty framework
    points = np.zeros(len(initial_vals), dtype=object)
    current_points = np.zeros(len(initial_vals), dtype=object)
    for i in range(len(initial_vals)):
        points[i], = ax.plot([], [], '.', color='black', alpha=0.05)
        current_points[i], = ax.plot([], [], '.', color='red', alpha=0.2, zorder=10)
    scale = np.sqrt(dvdt(t[0], V, W)**2 + dwdt(t[0], V, W)**2)
    qr = ax.quiver(V, W, dvdt(t[0], V, W)/scale, dwdt(t[0], V, W)/scale,
                   scale, cmap='winter_r', scale=20, width=0.005, zorder=3)
    title = ax.set_title('')


    def draw_frame(n):
        '''
        Commands to update parameters.
        Here, the phase portrait data points and quiver each frame.
        '''
        time_points = round(t_range/frame_num)
        frame_final_time = min(time_points*n+time_points, t_range-1)  # avoid index out of range
        for i in range(len(initial_vals)):
            points[i].set_data(ode_solns[i, :, :frame_final_time])
            current_points[i].set_data(*ode_solns[i, :, frame_final_time-1:frame_final_time])
        scale = np.sqrt(dvdt(t[frame_final_time], V, W)**2 + dwdt(t[frame_final_time], V, W)**2)
        qr.set_UVC(dvdt(t[frame_final_time], V, W)/scale, dwdt(t[frame_final_time], V, W)/scale, C=scale)
        title.set_text(f't = {t[frame_final_time] :.3f}')
        return fig,

    # create animation of given time length
    # note here we fit all the data points into the given animation time
    from matplotlib import animation
    frame_num = int(fps * anim_time)
    anim = animation.FuncAnimation(fig, draw_frame, frames=frame_num, interval=1000/fps, blit=True)
    
    plt.close()  # disable showing initial frame
    
    return anim

# convert animation to video (time-limiting step)
from IPython.display import HTML
anim = make_animation()  # uses custom function above
HTML(anim.to_html5_video() + '<style>video{width: 400px !important; height: auto;}</style>')

# convert animation to video (time-limiting step)
from IPython.display import HTML
anim = make_animation(t_range=int(t_len/3))  # uses custom function above
HTML(anim.to_html5_video() + '<style>video{width: 400px !important; height: auto;}</style>')