Root Finding Algorithms#
Teng-Jui Lin
Content adapted from UW AMATH 301, Beginning Scientific Computing, in Spring 2020.
Root finding algorithms
Bisection method
Newton’s method
Errors
scipyimplementationFinding root of scalar functions by
scipy.optimize.root_scalar()
As iterative methods, tolerance is set as a stopping criteria. The stopping criteria could be \(f(x_k) < \mathrm{tolerance}\), or it could also be \(|x_{k+1} - x_k| < \mathrm{tolerance}\).
Bisection method#
Goal: Given an internal \([a, b]\), find a root of \(f(x)\) in the interval.
Intermediate value theorem states that for continuous functions, if \(f(a)\) and \(f(b)\) have opposite signs, then there is some \(x\) between \(a\) and \(b\) such that \(f(x) = 0\).
Let midpoint be \(x=m\).
If \(f(m)\) and \(f(a)\) have opposite signs, then change the new interval to \([a, m]\).
If \(f(m)\) and \(f(b)\) have opposite signs, then change the new interval to \([m, b]\).
Implementation#
Problem Statement. Find the root of the function
using bisection method.
import matplotlib.pyplot as plt
import numpy as np
def bisection(f, left, right, tolerance=1e-6, max_iter=10000):
'''
Find a root of given function in an interval using bisection method.
:param f: objective function
:param left: lower bound of interval
:param right: upper bound of interval
:param tolerance: tolerance of stopping criteria
:param max_iter: maximum iteration allowed for calculation
:returns: root of objective function
'''
f_mid = tolerance * 2 # arbitrary number greater than tolerance
i = 0 # iteration counter
# bisection method logic
while abs(f_mid) > tolerance and i < max_iter:
mid = (left + right) / 2
f_mid = f(mid)
if f_mid == 0.0:
return mid
elif f_mid * f(left) < 0: # check sign change
right = mid
elif f_mid * f(right) < 0:
left = mid
else:
raise ValueError('f(a) and f(b) must have different signs')
i += 1
# maximum iteration warning
if i == max_iter:
import warnings
warnings.warn(f'Maximum iteration reached. Current stopping criteria is {abs(f_mid) :.2e}', UserWarning)
return mid
def test_func(x):
return x**3 + 5*x**2 - 2*x - 2
print(bisection(test_func, -2, 2))
-0.4797694683074951
Newton’s method#
Goal: Find a root of a function \(f(x)\) given an initial guess.
Using tangent line approximation, we have
Newton’s method uses the root of the tangent line approximation as the next guess (\(y=0\)), so we have
Therefore, the formula for Newton’s method is
Implementation#
Problem Statement. Find the root of the function
using Newton’s method.
def newton(f, df, x0, tolerance=1e-6, max_iter=10000):
'''
Find a root of given function using Newton's method with an initial guess.
:param f: objective function
:param df: derivative of target function
:param x0: initial guess of root
:param tolerance: tolerance of stopping criteria
:param max_iter: maximum iteration allowed for calculation
:returns: root of objective function
'''
i = 0 # iteration counter
x = x0
# newton's method logic
while abs(f(x)) > tolerance and i < max_iter:
x = x - f(x) / df(x)
i += 1
# maximum iteration warning
if i == max_iter:
import warnings
warnings.warn(f'Maximum iteration reached. Current stopping criteria is {abs(f(x)) :.2e}', UserWarning)
return x
def test_func(x):
return x**3 + 5*x**2 - 2*x - 2
def test_func_derivative(x):
return 3*x**2 + 10*x - 2
newton(test_func, test_func_derivative, 10)
0.7856670111986841
Root finding using scipy.optimize.root_scalar()#
scipy.optimize.root_scalar() can take various methods, each with their required input parameters.
from scipy.optimize import root_scalar
def test_func(x):
return x**3 + 5*x**2 - 2*x - 2
def test_func_derivative(x):
return 3*x**2 + 10*x - 2
# bisection method
root_scalar(test_func, bracket=[0, 1], method='bisect')
converged: True
flag: 'converged'
function_calls: 41
iterations: 39
root: 0.7856670111996209
# newton's method
root_scalar(test_func, x0=0, fprime=test_func_derivative, method='newton')
converged: True
flag: 'converged'
function_calls: 12
iterations: 6
root: -0.4797694818645718
# brent’s method
root_scalar(test_func, bracket=[0, 3], method='brentq')
converged: True
flag: 'converged'
function_calls: 13
iterations: 12
root: 0.7856670111980021
Assessing errors of root finding algorithms#
Problem Statement. Consider the function
Calculate an “exact” solution using
scipy.optimize’s Newton’s method and initial guess of \(x_0 = 0\).Find the root of \(f(x)\) using bisection method with interval of \([-100, 100]\) and a tolerance of \(10^{-8}\). Calculate the error at each step.
Find the root of \(f(x)\) using Newton’s method with an initial guess of \(x_0 = 100\) and a tolerance of \(10^{-8}\). Calculate the error at each step.
Plot and compare the errors of bisection and Newton’s method.
## problem 1
def f(x):
return x**5 - 3*x**4 + 5*x**3 - 7*x**2 + 6*x - 2
def df(x):
return 5*x**4 - 12*x**3 + 15*x**2 - 14*x + 6
x0 = 100
exact = root_scalar(f, x0=100, fprime=df, method='newton').root
print(f'The "exact" solution is {exact}')
The "exact" solution is 1.0000089368806895
## problem 2 - bisection method
mids = []
bisection_errors = []
left = -100
right = 100
tolerance = 1e-8
max_iter = 1000
f_mid = tolerance * 2 # arbitrary number greater than tolerance
i = 0 # iteration counter
# bisection method logic
while abs(f_mid) > tolerance and i < max_iter:
mids.append((left + right) / 2)
f_mid = f(mids[i])
bisection_errors.append(abs(exact - mids[i]))
if f_mid == 0.0:
break
elif f_mid * f(left) < 0: # check sign change
right = mids[i]
elif f_mid * f(right) < 0:
left = mids[i]
else:
raise ValueError('f(a) and f(b) must have different signs')
i += 1
mids[-1]
1.0009765625
## problem 3 - newton's method
x = [100]
newton_errors = [abs(exact - x[0])]
i = 0 # iteration counter
# newton's method logic
while abs(f(x[i])) > tolerance and i < max_iter:
x.append(x[i] - f(x[i]) / df(x[i]))
newton_errors.append(abs(exact - x[i+1]))
i += 1
x[-1]
1.0014079515589658
## probelm 4
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.rcParams.update({
'font.family': 'Arial', # Times New Roman, Calibri
'font.weight': 'normal',
'mathtext.fontset': 'cm',
'font.size': 18,
'lines.linewidth': 2,
'axes.linewidth': 2,
'axes.spines.top': False,
'axes.spines.right': False,
'axes.titleweight': 'bold',
'axes.titlesize': 18,
'axes.labelweight': 'bold',
'xtick.major.size': 8,
'xtick.major.width': 2,
'ytick.major.size': 8,
'ytick.major.width': 2,
'figure.dpi': 80,
'savefig.dpi': 300,
'legend.framealpha': 1,
'legend.edgecolor': 'black',
'legend.fancybox': False,
'legend.fontsize': 14
})
fig, ax = plt.subplots(figsize=(6, 4))
ax.semilogy(np.arange(1, len(bisection_errors)+1), bisection_errors, 'o', label='Bisection method', alpha=0.8)
ax.semilogy(np.arange(len(newton_errors)), newton_errors, '^', label="Newton's method", alpha=0.8)
ax.set_xlabel('Iterations')
ax.set_ylabel('Error')
ax.set_title('Error of root finding algorithms')
ax.set_xlim(0)
ax.legend()
<matplotlib.legend.Legend at 0x1af3056a948>
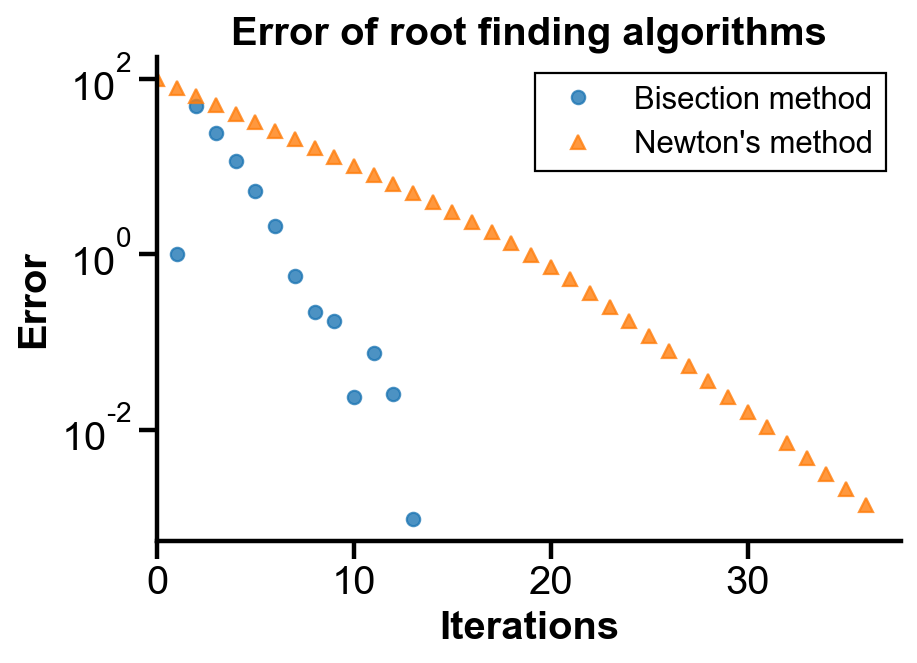
Comment. In this case, bisection method converges more rapidly than Newton’s method, as shown in the steeper negative slope. The trend is not universal: it depends on the function, initial guess, and given interval. generally, Newton’s method is faster than bisection if proper initial guess is chosen. However, Newton’s method may be slow when the derivative of the function is zero at the root. It would also just doesn’t work if the function is ill-conditioned. Also, analytical expression of derivative is needed for Newton’s method.